The Binomial Expansion Theorem is an algebra formula that describes the algebraic expansion of powers of a binomial According to the binomial expansion theorem, it is possible to expand any power of x y into a sum of the termsExpand the equation (xy1)3 talentpuno09 talentpuno09 Math Junior High School answered • expert verified Expand the equation (xy1)3 PlsLearn about expand using our free math solver with stepbystep solutions
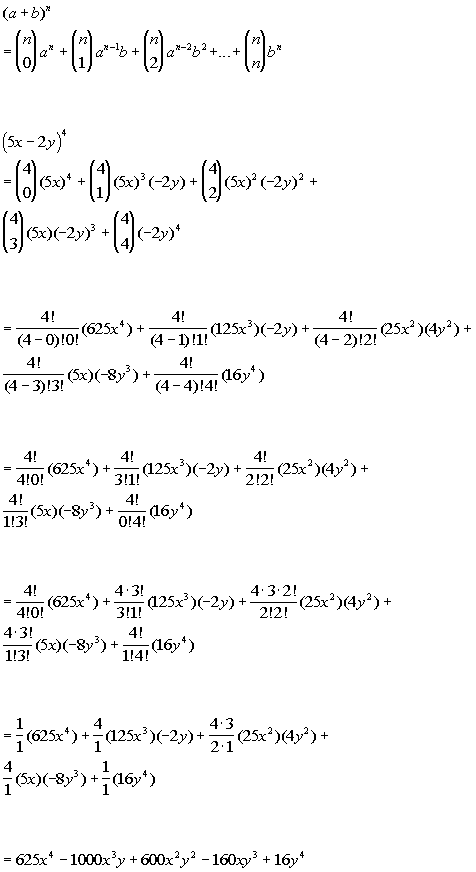
Tutorial 54 The Binomial Theorem
(x-y)^3 expand formula
(x-y)^3 expand formula-👉 Learn all about sequences In this playlist, we will explore how to write the rule for a sequence, determine the nth term, determine the first 5 terms or画像をダウンロード (xy)^3 expand formula 2597(3xy)^3 expand Factor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = (a b) (a 2 a b b 2) where a = x a = x and b = y b = y (x−y)(x2 xyy2) (x y) (x 2 x y y 2)Binomial Expansions Binomial



Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths
The following are algebraix expansion formulae of selected polynomials Square of summation (x y) 2 = x 2 2xy y 2 Square of difference (x y) 2 = x 2 2xy y 2 Difference of squares x 2 y 2 = (x y) (x y) Cube of summation (x y) 3 = x 3 3x 2 y 3xy 2 y 3Result A sum containing 2 terms;Expand (xy)^3 full pad » x^2 x^ {\msquare} \log_ {\msquare} \sqrt {\square} \nthroot \msquare {\square} \le \ge
The simplify command finds the simplest form of an equation Simplifyexpr,assum does simplification using assumptions Expandexpr,patt leaves unexpanded any parts of expr that are free of the pattern patt ExpandAllexpr expands out all products and integer powers in ant part of exps ExpandAllexpr,patt avoids expanding parts of expr that do not contain terms matching According to the binomial theorem, it is possible to expand the polynomial (x y)^n as a sum having terms in the form of an x b is, where the exponents b and c are positive integers with b c = n The binomial expansion formula is given byExpand (xy)^3 (x y)3 ( x y) 3 Use the Binomial Theorem x3 3x2y3xy2 y3 x 3 3 x 2 y 3 x y 2 y 3
Expand this algebraic expression `(x2)^3` returns `2^33*x*2^23*2*x^2x^3` Note that the result is not returned as the simplest expression in order to be able to follow the steps of calculations To simplify the results, simply use the reduce function Special expansions online The function expand makes it possible to expand a product, itFind the coefficient of x^7 for (x3)^11 Use the binomial theorem to expand (2y3x)^5 Prove that (n over r)= (n over nr) for all integers where n is greater than or equal to r and r is greater than or equal to zero Prove that (n over n2) ( n1 over1 2 1 for n = 2 the x^2 term is the rightmost one here so we'll get 1 times the first term to the 0 power times the second term squared or 1*1^0* (x/5)^2 = x^2/25 so not here 1 3 3 1 for n = 3 Squared term is second from the right, so we get 3*1^1* (x/5)^2 = 3x^2/25 so not here 1



Is There A Shortcut To Expand The Equation X Y Quora




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9
#(xy)^3=(xy)(xy)(xy)# Expand the first two brackets #(xy)(xy)=x^2xyxyy^2# #rArr x^2y^22xy# Multiply the result by the last two brackets #(x^2y^22xy)(xy)=x^3x^2yxy^2y^32x^2y2xy^2# #rArr x^3y^33x^2y3xy^2#The Binomial Theorem is a formula that can be used to expand any binomial (xy)n =∑n k=0(n k)xn−kyk =xn(n 1)xn−1y(n 2)xn−2y2( n n−1)xyn−1yn ( x y) n = ∑ k = 0 n ( n k) x n − k y k = x n ( n 1) x n − 1 y ( n 2) x n − 2 y 2 ( n n − 1) x y n − 1 y nOBJECTIVES Find the product of two binomials Use the distributive property to multiply any two polynomials In the previous section you learned that the product A (2x y) expands to A (2x) A (y) Now consider the product (3x z) (2x y) Since (3x z) is in parentheses, we can treat it as a single factor and expand (3x z) (2x y) in




Learn Algebraic Identity Of X Y And X Y In 3 Minutes



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomialAccording to the theorem, it is possible to expand the polynomial (x y) n into a sum involving terms of the form ax b y c, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positive= and so the power series expansion agrees with the Taylor series Thus a function is analytic in an open disk centred at b if and only if its Taylor series converges toAn outline of Isaac Newton's original discovery of the generalized binomial theorem Many thanks to Rob Thomasson, Skip Franklin, and Jay Gittings for their



Http Www2 Southeastern Edu Academics Faculty Talwis Teaching Expandfactor Pdf




Polynomial Expansion And Pascal S Triangle Ck 12 Foundation
If a binomial expression (x y) n is to be expanded, a binomial expansion formula can be used to express this in terms of the simpler expressions of the form ax by c in which 'b' and 'c' are non negative integers The value of 'a' completely depends on the value of 'n' and 'b'Expand the equation (xy1)3 Pls i need it ASAP Answer by Guest Answer #Answerfortrees Rate answer Answer by Guest x^33x^2y3xy^2y^33x^26xy3y^23x3y1 Rate answer Wrong answer?Now, we have the coefficients of the first five terms By the binomial formula, when the number of terms is even, then coefficients of each two terms that are at



Expanding Polynomial Factors Maths First Institute Of Fundamental Sciences Massey University




Using The Binomial Theorem College Algebra
Expand the formula of (xy)^3 Get the answers you need, now!The Binomial Theorem is the method of expanding an expression which has been raised to any finite power A binomial Theorem is a powerful tool of expansion, which has application in Algebra, probability, etc Binomial Expression A binomial expression is an algebraic expression which contains two dissimilar terms Ex a b, a 3 b 3, etc (xy)3 expand it as formula phaniraja92 phaniraja92 Math Secondary School (xy)3 expand it as formula 2 See answers vasudevmolleti0676 vasudevmolleti0676
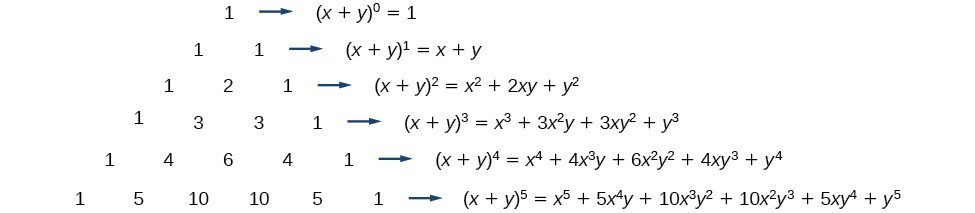



Using The Binomial Theorem College Algebra




X Y 3 Identity Novocom Top
If your question is not fully disclosed, then try using the search on the site and find other answers on the subject MathThe base is X;(xyz)^3 put xy = a (az)^3= a^3 z^3 3az ( az) = (xy)^3 z^3 3 a^2 z 3a z^2 = x^3y^3 z^3 3 x^2 y 3 x y^2 3(xy)^2 z 3(xy) z^2 =x^3 y^3 z^3 3 x



Factorials To Binomial Theorem



Www Kentschools Net Leyring Files 17 03 8 4 New Pdf
The exponent is two;Algebra Factor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y Differentiating by x the above formula n times, then setting x = b gives ()!




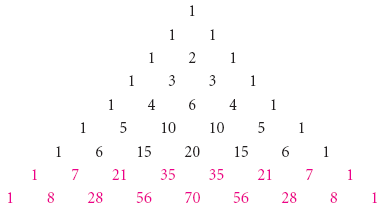
How To Calculate X Y N With Pascal S Triangle 9 Steps




Table 1 From Generalized Ismail S Argument And F G Expansion Formula Semantic Scholar
SolutionShow Solution ( x y z ) 2 = x 2 y 2 z 2 2 (x) (y) 2 (y) (z) 2 (z) (x) = x 2 y 2 z 2 2xy 2yz 2zx Concept Expansion of Formula Report ErrorThe first term of the sum is a power;(x y) 7 = x 7 7x 6 y 21x 5 y 2 35x 4 y 3 35x 3 y 4 21x 2 y 5 7xy 6 y 7 When the terms of the binomial have coefficient(s), be sure to apply the exponents to these coefficients Example Write out the expansion of (2 x 3 y ) 4




Learn Algebraic Identity Of X Y And X Y In 3 Minutes
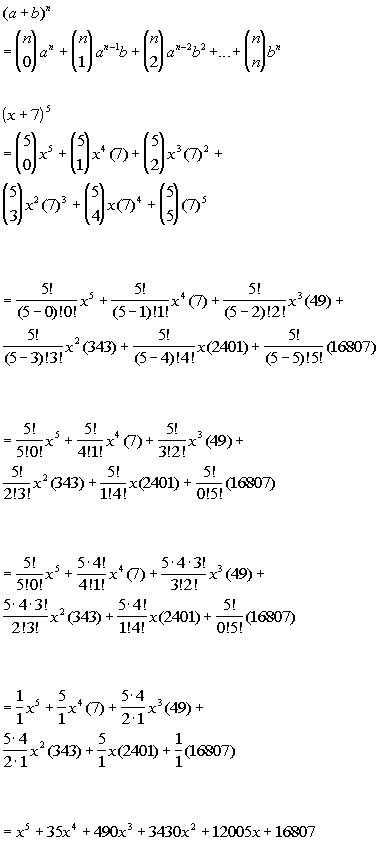



Tutorial 54 The Binomial Theorem
X exponentiated by two plus negative Y raised to the power two ;About the Author Davneet Singh Davneet Singh is a graduate from Indian Institute of Technology, Kanpur(xy)^3 expand 1×4 2xyx2 x2y2 2xyx2 4x2y2 2xyy2 y2x2 y22xy 1y4 073 073 033The binomial theorem states abn n k0nCkankbk a b n k 0 n Type in any equation to get the solution steps and graph Expand3x6 expand2xxa expand2x4x5




Section 3 3 Binomial Coefficients 30 Points 5 Bonus Chegg Com




What Is The Formula For A B 6 Quora
We're going to look at the Binomial Expansion Theorem, a shortcut method of raising a binomial to a power (xy) 4 = x 4 4x 3 y 6x 2 y 2 4xy 3 y 4 (xy) 5 = x 5 5x 4 y 10x 3 y 2 10x 2 y 3 5xy 4 y 5 There are several things that you hopefully have noticed after looking at the expansion The n and r in the formula standPdf On The Solution Of Diophantine Equation X 3 Y 3 Z 2 Then type the at symbol Multiply each term in by 2x315 at x6 clickable demo try entering 2x315 at x6 into the text box X y3 Tap for more steps Multiply each term in by Free math problem solver answers your algebra geometry trigonometry calculus and statistics homework questions withExpand the expression of log5x^(1/3)y^6 5 is the base of the log this is pretty tricky stuff and im not sure how to attempt it Vectors Expand to the general case to explore how the cross product behaves under scalar multiplication k (a x b) = (ka) x b = a x (kb)




X 3 Y 3 X 3 Y 3 Formula Proof Youtube




X Y 2 3 Find The Expansion Of The Following Brainly In
Binomial Theorem to expand polynomials explained with examples and several practice problems and downloadable pdf worksheet (x y) 4 = x 4 4x 3 y 6x 2 y 2 4xy 3 y 4;The exponent is two; You can check the formulas of A plus B plus C Whole cube in three ways We are going to share the (abc)^3 algebra formulas for you as well as how to create (abc)^3 and proof we can write we know that what is the formula of need too write in simple form of multiplication Simplify the all Multiplication one by one



1




Don T Understand Why This Binomial Expansion Is Not Valid For X 1 Mathematics Stack Exchange
Expand (x y z)^2 formulaFor any fixed α ∈ C, we have the Newtonian expansion (1 x) α = 1 α x α (α − 1) 2!Expand the following product (3 x 1) (2 x 4) `(3x1)(2x4)` returns `3*x*2*x3*x*42*x4` Expand this algebraic expression `(x2)^3` returns `2^33*x*2^23*2*x^2x^3` Note that the result is not returned as the simplest expression in orderThe formula is (xy)³=x³y³3xy(xy) Proof for this formula step by step =(xy)³ =(xy)(xy)(xy) ={(xy)(xy)}(xy) =(x²xyxyy²)(xy) =(xy)(x²y²2xyThe second term of the sum is equal to a negative power;




What Is The Formula Of Math A B 3 Math Quora




The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreWhen we have a sum (difference) of two or three numbers to power of 2 or 3 and we need to remove the brackets we use polynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2آلة حاسبة للتوسيع والتبسيط وسّع وبسّط التعابير الجبريّة خطوة بخطوة




3 Expand With The Help Of Formula X Y 3 2




How Do You Expand The Binomial X Y 5 Socratic
Expand\3(x6) expand\2x(xa) expand\(2x4)(x5) expand\(2x5)(3x6) expand\(4x^23)(3x1) expand\(x^23y)^3 (xy)^3 formulaThe equation x y z = 1 describes some collection of points in R3 Describe and sketch the points that satisfy x y z = 1 and are in the xy plane, in the xz plane, and in the yz plane 6 Find the lengths of the sides of the triangle with vertices (1,0,1), (2,2,−1), and (−3,2,−2)The author is saying y is not a particular numberExpand the binomial using the binomial formula (2 x3 y)^{3} Meet students taking the same courses as you are!Join a Numerade study group on Discord Expand the binomial using the binomial formula $$(2 x3 y)^{3}$$ Answer $(2 x3 y)^{3}=8 x^{3}36 x^{2} y54 x y^{2}27 y^{3}$ Topics Introduction to Sequences and Series Introduction to




Expand 1x Y3 3 Maths Questions




Baker Campbell Hausdorff Formula Wikipedia
The base is Y; Cube Formulas (a b) 3 = a 3 b 3 3ab(a b) (a − b) 3 = a 3 b 3 3ab(a b) a 3 − b 3 = (a Decimal Expansion;In mathematics, the cube of sum of two terms is expressed as the cube of binomial x y It is read as x plus y whole cube It is mainly used in mathematics as a formula for expanding cube of sum of any two terms in their terms (x y) 3 = x 3 y 3 3 x 2 y 3 x y 2
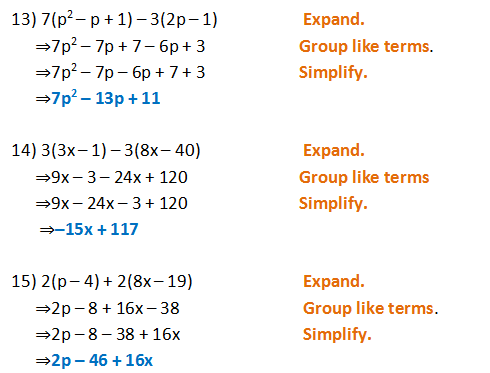



Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths
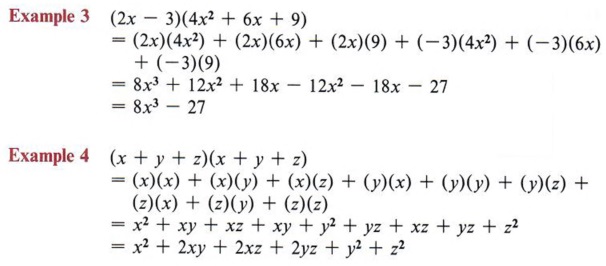



Expand Expand Terms Multiply Polynomials With Step By Step Math Problem Solver
The binomial expansion of a difference is as easy, just alternate the signs (x y) 3 = x 3 3x 2 y 3xy 2 y 3In general the expansion of the binomial (x y) n is given by the Binomial TheoremTheorem 671 The Binomial Theorem top Can you see just how this formula alternates the signs for the expansion of a difference?Click here👆to get an answer to your question ️ \"3) Expand with the help of formula \\( ( x y 3 ) ^ { 2 } \\)\"




3 The Formula For The Taylor Expansion Of The Second Chegg Com




Expand And Simplify Binomial Squares 2x 3y 2 Youtube
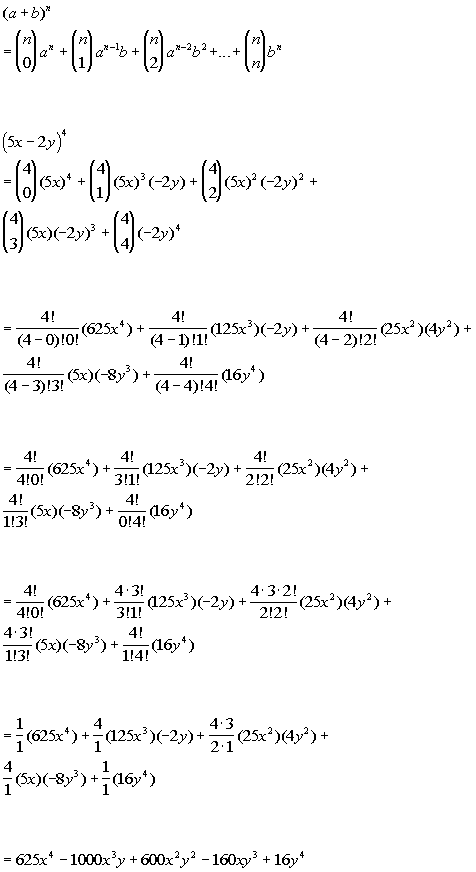



Tutorial 54 The Binomial Theorem
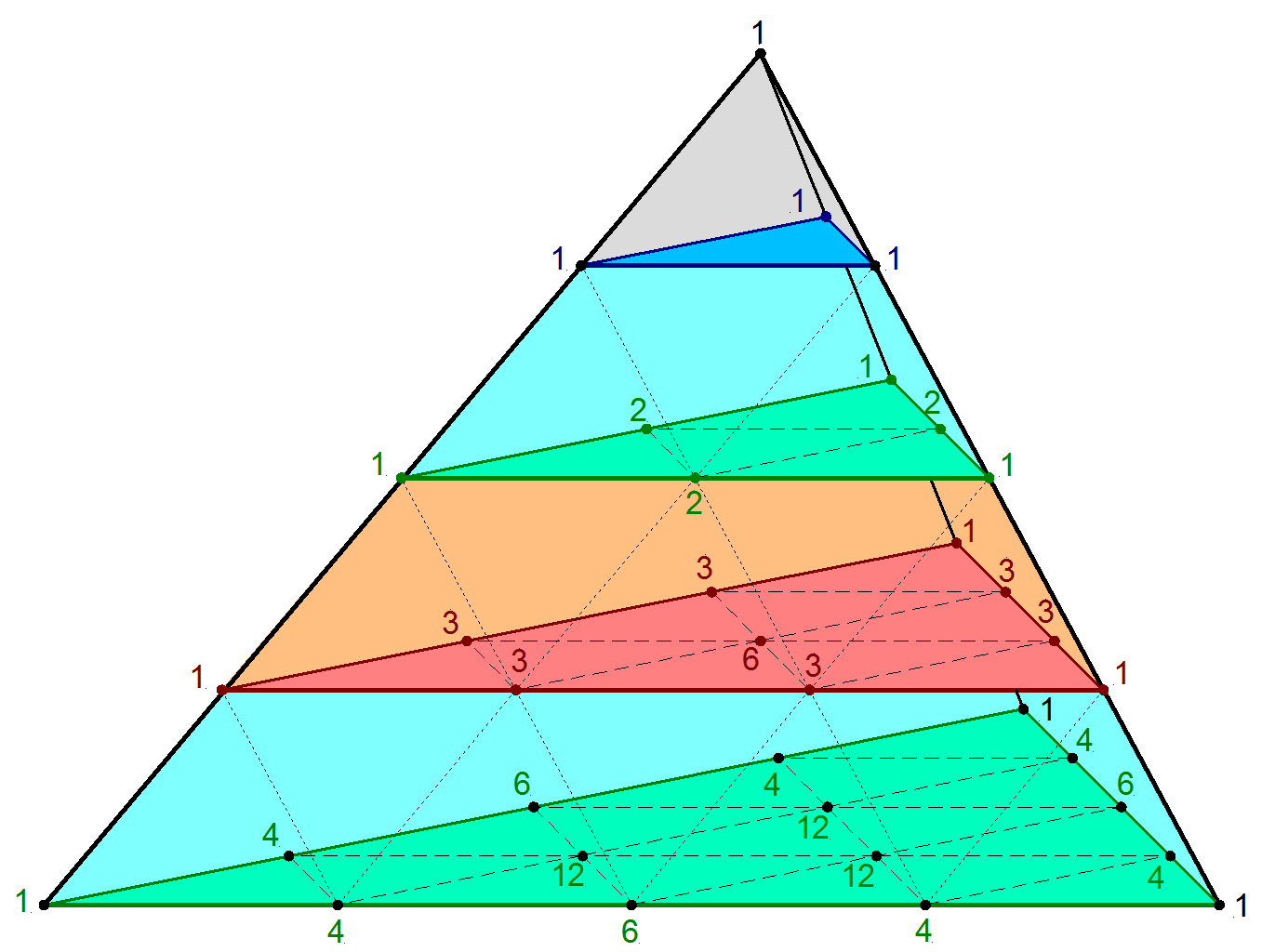



Pascal S Pyramid Wikipedia




Binomial Expansion 1 X 3 Formula Novocom Top




Three Variables Cubic Polynomial Formulas Maths Solutions Quadratics Quadratic Equation



Www Kentschools Net Leyring Files 17 03 8 4 New Pdf




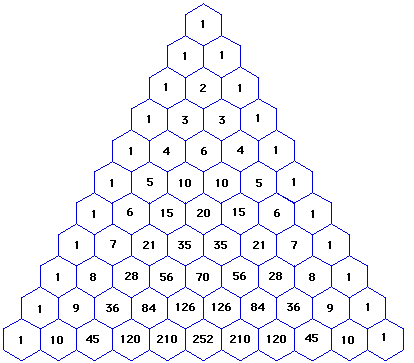
Pascal S Triangle And The Binomial Theorem
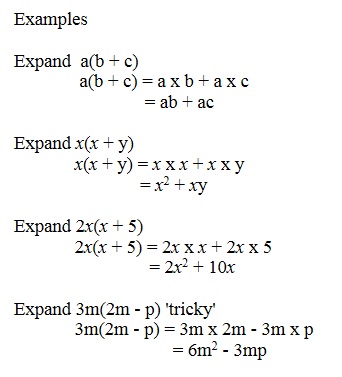



Algebra 5 Expanding Simplifying Mathtec




Properties Of Logarithms Algebra Ii Quiz Quizizz




The Binomial Theorem Defining Expressions Video Lesson Transcript Study Com




9 Binomial Theorem Example 4 Expanding 3 Terms In A Binomial Question Youtube



If Math X Y 3 Math And Math X 2 Y 2 3 Math Then What Is The Value Of Math X 2 Y 2 Math Quora




How To Calculate X Y N With Pascal S Triangle 9 Steps




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




9 5 The Binomial Theorem




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9
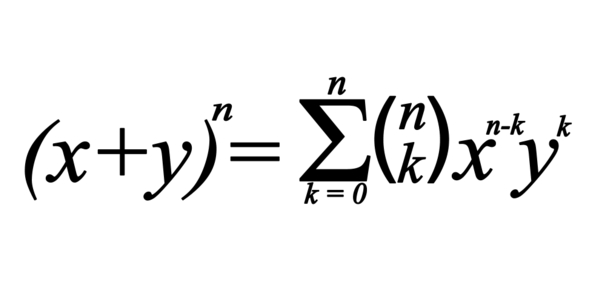



Binomial Theorem Quiz Proprofs Quiz




How Can We Expand X Y 1 2 Youtube



4 The Binomial Theorem




Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5
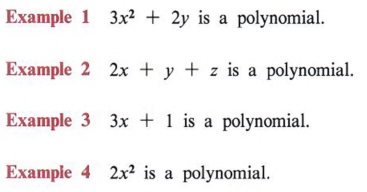



Expand Expand Terms Multiply Polynomials With Step By Step Math Problem Solver




Expanding Algebraic Expressions Using Identities Worksheets




A B N And A B N Formula Expander




Expand X Y 3 Solved



How Do You Expand X Y 10 Socratic



A Lesson In Making Use Of Structure From With Jmccalla1 Experiments In Learning By Doing




Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf
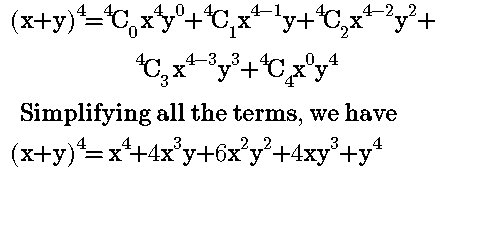



Worked Examples On Binomial Expansion Steemit



Expand X Y Z Square Brainly In




Section 8 5 The Binomial Theorem Ppt Download



What Is The Answer Of X Y Quora




Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo



Search Q X Y 5e3 Identity Tbm Isch




How Do You Use The Binomial Theorem To Expand X Y 5 Socratic
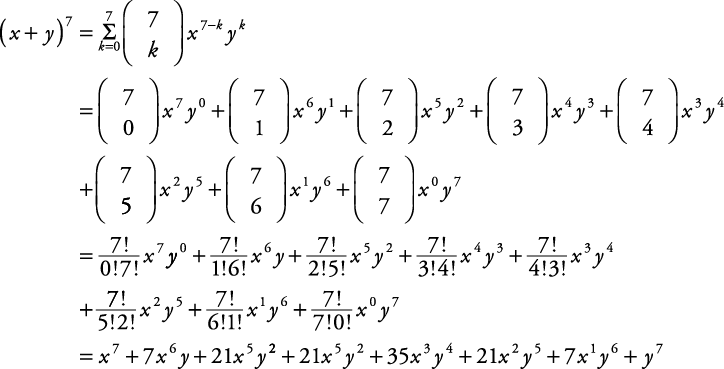



Binomial Coefficients And The Binomial Theorem




Taylor S Series Expansion An Overview Sciencedirect Topics




Don T Understand Why This Binomial Expansion Is Not Valid For X 1 Mathematics Stack Exchange




Solved Question 2 46 Marks 2 1 Expand And Simplify The Chegg Com
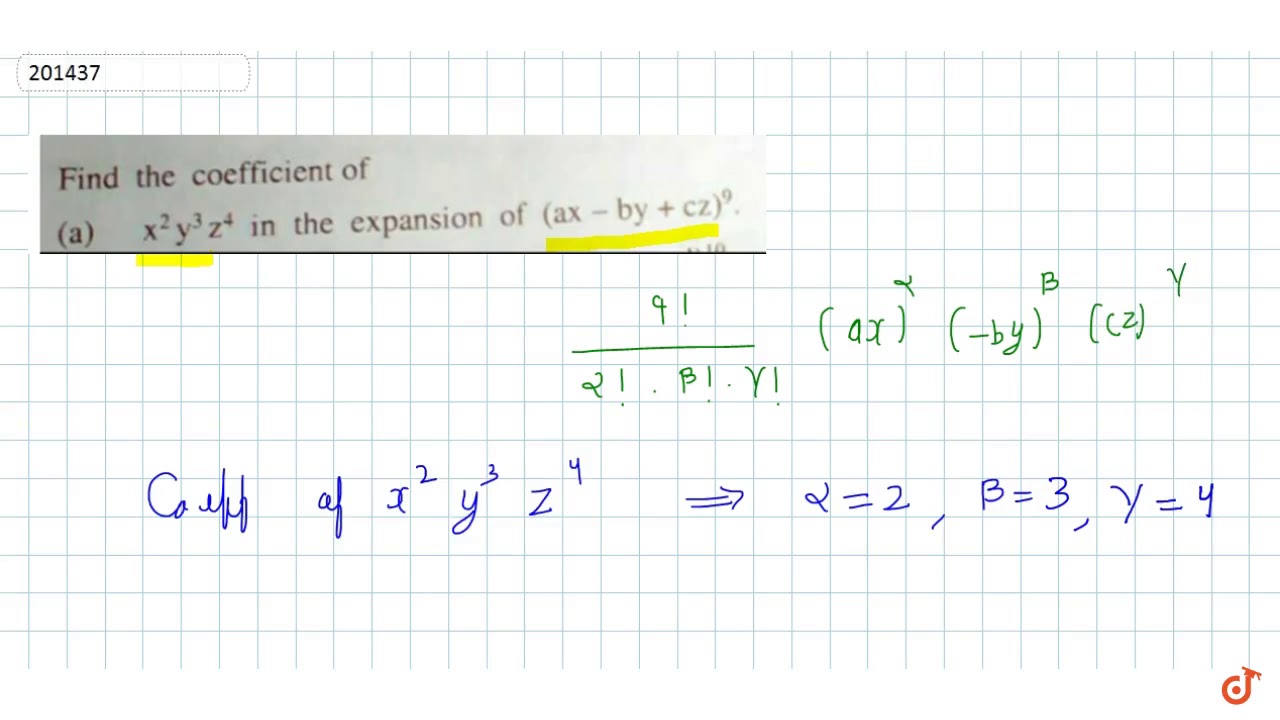



Find The Coefficient Of X 2 Y 3 Z 4 In The Expansion Of Ax By Cz 9 Youtube
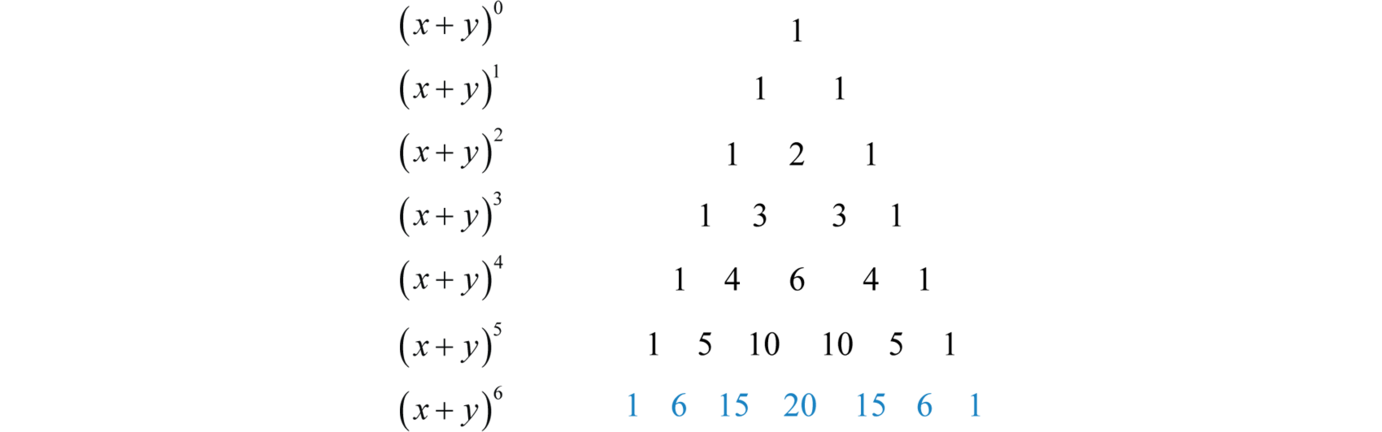



Binomial Theorem




Section 8 5 The Binomial Theorem Ppt Download
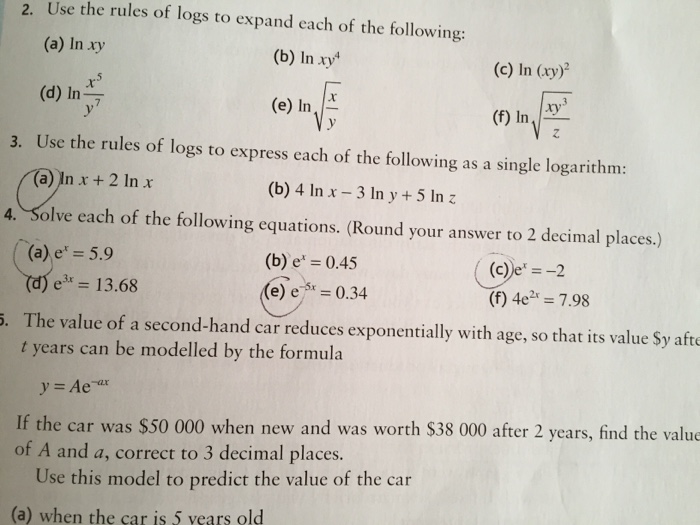



Solved 2 Use The Rules Of Logs To Expand Each Of The Fol Chegg Com




Expand The Given Expression 3 X3 X Y 4 Z 33 X Gauthmath



Is There A Shortcut To Expand The Equation X Y Quora




The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium




A Quick And Efficient Way To Expand Binomials Ppt Download




Using The Binomial Theorem College Algebra




X 2 3 Expand Formula Novocom Top
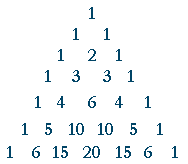



Binomial Theorem Topics In Precalculus



Expand 1 X Y 3 Whole Cube Studyrankersonline



1




Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf




Expanding Binomials Video Polynomials Khan Academy




How Do You Expand X Y 6 Using Pascal S Triangle Socratic



1




Binomial Expansion Formulas Derivation Examples
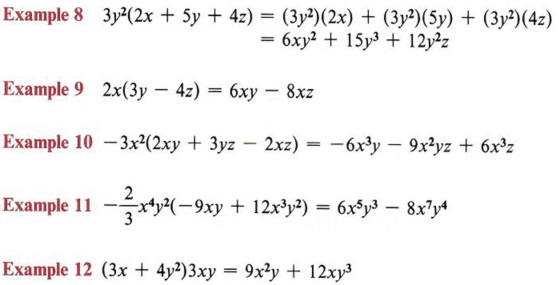



Expand Expand Terms Multiply Polynomials With Step By Step Math Problem Solver
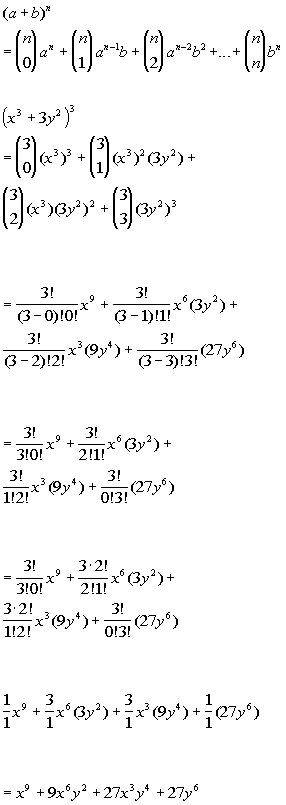



Tutorial 54 The Binomial Theorem




Expand Each Of The Following I X 2 Y 3 2 Ii X 5 X 3




Binomial Theorem




Problem 3 10 Points Consider The Ode Y Xy 2y Chegg Com




Answered Qi N Expand With Binomial Formula 1 Bartleby




Ml Aggarwal Solutions For Class 9 Chapter 3 Expansions Download Free Pdf




Expand 1 X Y 3 3 Solve It Fastly Brainly In




1 Expand F X Y Xº Y About The Point 0 0 Using Taylor S Series Formula2 Find The Maximum And Brainly In




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Binomial Theorem Formula Properties Examples




Expanding Logarithms




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




9 9 Pts A State The Binomial Theorem B Find Chegg Com
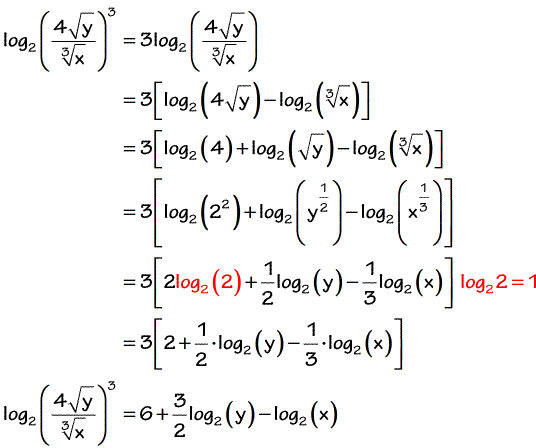



Expanding Logarithms Chilimath



What Is The Binomial Expansion For 1 X 1 Quora
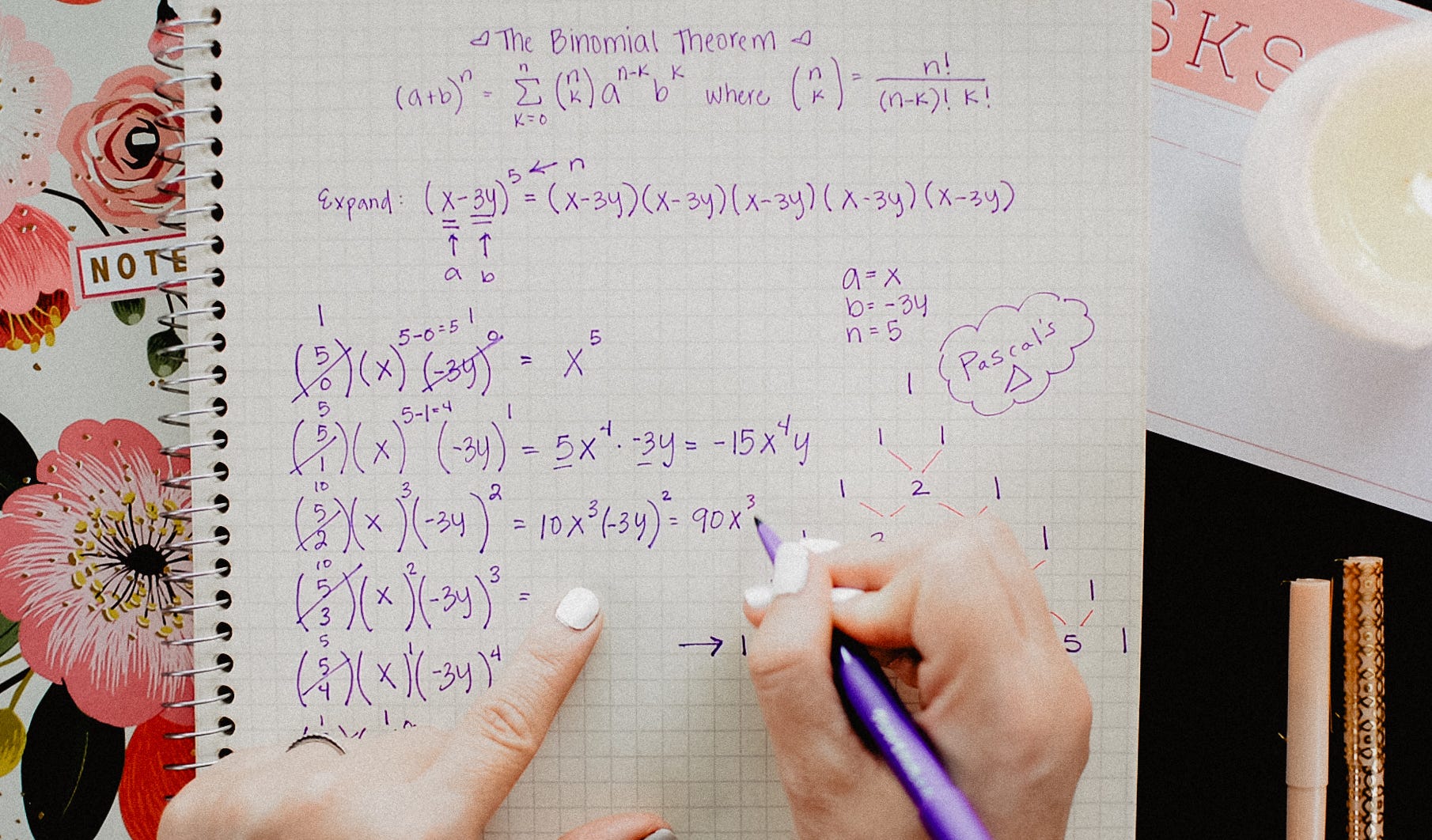



The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium



0 件のコメント:
コメントを投稿